
Edward Winter
What constitutes a combination? Many books claim that a sacrifice is essential, but C.J.S. Purdy used the following position to dispute that:

White, to play, wins by 1 Bb5+ Ke7 2 Nf5+ Ke6 3 Nxg7+, etc. He has made no sacrifices but ‘a succession of threats winding up with the capture of the netted piece’. See page 201 of C.J.S. Purdy: His Life, His Games and His Writings by J. Hammond and R. Jamieson (Melbourne, 1982).
Other illustrative positions would be welcome. Do readers agree with Purdy that ‘Combinations are characterized by violent moves, but not necessarily sacrifices’?

(1960)
Lawrence Stevens (Pasadena, CA, USA) concurs that a combination does not necessarily contain a sacrifice:
‘What are being “combined” are the powers of more than one piece and/or forcing moves. I would think that the sacrificial characterization evolved through usage, i.e. it was statistically likely that a sacrifice had occurred.’
From Robert S. Moore (Anchorage, AK, USA):
‘Cecil Purdy seems to me to be defending an exceptionally doubtful thesis that “combinations” do not require a sacrifice. Admittedly, in his chosen example we see a number of combinational elements – line clearance, overworked pieces and a mating net – but all of the moves given would likely be found, although perhaps without fully realizing their implications in advance, by the merest beginner. Sacrifice is the drama, the surprise, the brilliance and the dignity of a combination; it is that which lifts it above being only an illustration of the elements. In Purdy’s own example, 3 Bc4 (instead of 3 Nxg7+) is a minor combination.’
From Philip Laren (Irmo, SC, USA):
‘I was first shown the position in C.N. 1960 a few years ago by Ron Finegold, who asked me to find the best continuation. It doesn’t take a super Grandmaster to figure out that 3 Bc4! is a) a sacrifice, b) objectively better than 3 Nxg7+ and c) much more aesthetically pleasing.’
Ron Evers (Bar Harbor, ME, USA) writes:
‘My personal definition: “A combination is a sequence of moves that forces together (combines) two or more tactical themes.” Purdy’s example, therefore, is a combination because it forces together, by an attack on the king, two tactical themes: decoy and double attack. Sacrifice in a combination is the method of applying force. “You know of course that attacks and threats of all kinds, exchanges and Zugzwang are such means of applying force, but the most lasting effects are achieved with sacrifices.” This quote is from Yuri Averbakh’s Chess Tactics for Advanced Players, page 212. An example on page 209 proves to me that a sacrifice is not needed in a combination.’
Robert John McCrary (Columbia, SC, USA) sends us a copy of the July 1989 issue of the Magazine of the SC Chess Association, in which (pages 14-15) he contributed an article that defined ‘combination’ as follows:
‘A combination is a precisely-identified set of variations at least three half-moves deep, leading to a precise set of objectives, with the same player moving first and last in all the variations, and with his opponent having a choice of at least two defences leading, respectively, to distinct outcomes.’
A contribution from Antonio Gude (Madrid):
‘I believe that Purdy is mistaken about the position with which he claims to illustrate his interesting thesis, because White wins by following a logical tactical sequence which should not be regarded as a combination. A position that provides a better illustration of his theory comes from the game Ivan Sokolov v Lembit Oll (Wijk aan Zee, 1993), after Black’s 29th move. White plays an extraordinarily strong move (30 Qc8). Owing to the strength of White’s finish, we can call it a combination, since it is surprising and effective. However, it is also the consequence of an earlier combination, which did involve sacrifices.’

30 Qc8 Qd7 31 Re1+ Qe6 32 Rxe6+ fxe6 33 f7+ Resigns.
We add two other views:
a) ‘A combination has nothing to do with sacrifice, but, of course, there are sacrificial combinations just as there are combinations which are designed to win an opponent’s pieces or bring about an accession of material.’ (W.H. Watts, writing on page 14 of Chess Pie No. 3 (London, 1936).)
b) ‘What is combination? Nothing but the logical weaving together of ideas.’ (J.N. Hanks, Chess World, February 1960, page 25.)
(2035)
Taking the example of a 1932 Spielmann v Stoltz game, C.N. 2035 (see pages 208-209 of Kings, Commoners and Knaves) asked whether the definition of ‘combination’ should cover combinative hallucinations.
Not according to Emanuel Lasker, who wrote on page 153 of Lasker’s Manual of Chess (New York, 1927):
‘A combination must be sound. An unsound combination is no combination at all. It is merely an attempt, an error, a failure, a nonentity.’
The remark is in the Third Book, after a Tartakower-Alekhine position. The text in various German editions (page numbers vary):
‘Eine Kombination muß richtig sein, sonst ist sie nur ein Versuch, ein Fehlgriff, ein Irrtum, und eigentlich ein Unding.’
(11191)
Publishing the next game on pages 280-281 of its September 1905 issue, the Deutsche Schachzeitung described the finish as ‘an original nine-move combination winning the enemy queen’.
Frank James Marshall – E. Pécher
Brussels, 22 May 1905
Danish Gambit
1 e4 e5 2 d4 exd4 3 c3 dxc3 4 Bc4 cxb2 5 Bxb2 Bb4+ 6 Nc3 Nc6 7 Nf3 Nf6 8 e5 Qe7 9 O-O Bxc3 10 exf6 Qxf6 11 Re1+ Kd8 12 Bxc3 Qxc3 13 Qd5 d6 14 Rac1 Qf6 15 Ng5 Be6 16 Nxe6+ fxe6 17 Rxe6 Qf4 18 Rce1 Rf8 19 Kh1 Kd7 20 Bd3 Rae8

21 Rxe8 Rxe8 22 Bf5+ Kd8 23 Rxe8+ Kxe8 24 Qg8+ Ke7 25 Qxg7+ Ke8 26 Qg8+ Ke7 27 Qe6+ Kf8 28 Qf6+ Resigns.
(Kingpin, 1997)
When was ‘combination’ first used as a chess term, and in which language?
As regards English, the Oxford English Dictionary (which has the definition ‘an ingenious sequence of moves in chess’) offers as its earliest citation ‘Mr Blackburne is not apt to lag when the opportunity for a fine combination presents itself’ on page 469 of The Field, 15 May 1875. However, we would mention that in the London Era, 1858 J. Löwenthal wrote as follows concerning 21 Rf3 in Morphy v Baucher, Paris, 1858:
‘The commencement of a brilliant combination, worthy of the immortal Labourdonnais, with board and men before him, and marvellous when we consider that Mr Morphy was playing blindfolded, and conducting at the same time seven other difficult games.’
Information on the exact issue and page number of Era would be appreciated, since we have only a reprint of the column in an 1858 US newspaper.
‘Combination’ was also used by Löwenthal when annotating the
Morphy v Baucher game on page 185 of his book Morphy’s Games
of Chess (London, 1860), but how much further back can the
term be traced, in any language?
(5001)
The Löwenthal observation was on page 5 of the Era edition of 3 October 1858.
From page 85 of Chess by Easy Stages by E.G.R. Cordingley (London, 1945):
‘Combination: A series of two or more moves combining the action of two or more men against a transitory weakness with the object of gain.’
The definition of combination on page 211 of Chess by Bill Hartston (London, 1996):
‘A sequence of moves involving more than one piece that leads to strategic or tactical gains.’
Ola Winfridsson (São Paulo, Brazil) suggests that a particularly apt and lucid explanation of what constitutes a combination is on pages 12-16 of volume one of Complete Chess Strategy by L. Pachman (London, 1975), where two well-known positions were discussed:

Důras v Barász, Breslau, 1912 (before 35 Rxd6)

Nimzowitsch v Rubinstein, Dresden, 1926 (before 18 Nh1)
Our correspondent remarks that Pachman makes a distinction between ‘manoeuvre’ and ‘forcing manoeuvre’ (the latter forces certain replies by the opponent), and that the book states on pages 15-16:
‘A forcing manoeuvre which is based on certain strategic contradictions is called a combination. This term is very often confused with sacrifice, but this is wrong for two reasons.
Firstly, because the strategic contradiction which is the basis of every combination does not necessarily involve the sacrifice of material. The side carrying out a manoeuvre may accept a certain positional disadvantage such as a weak pawn, the exchange of a well-placed piece, an exposed king, etc. These and similar freely accepted positional disadvantages are of course just as much strategic contradictions. During the rest of the manoeuvre the active side reaches a position which is more advantageous than the original one, and this again is the hallmark of a combination, although sacrifice does not come into it.
Secondly, there are sacrifices which are in no way connected with a manoeuvre. In our chapter “The value of the pieces” we shall demonstrate that the value of individual pieces is relative, depending upon the kind of position they are in. We shall then see “positional” or “strategic” sacrifices which are not part of a combination but arise from considerations about the effectiveness of certain pieces.’
(8067)
A detailed attempt to define a chess combination was made by Georges Renaud on page 59 of the November 1927 Chess Amateur (in a translation from a series of articles by Renaud which had begun in L’Eclaireur du Soir on 31 August 1927):
‘A “combination” is a manoeuvre obtaining for the player who executes it – and without the adversary having any effective defence if the combination is sound – a certain advantage such as the gain of material (a pawn, the exchange, a piece), a mating attack, improvement of the position, and finally (in the case of starting from an inferior position) a draw by stalemate, perpetual check, or reduction of force below mating strength.
A combination in the minds of many amateurs is something hidden and necessitating a sacrifice. Both these conditions are absolutely superfluous.’
(8695)
‘Combination is defined as two or more moves having a common object, whether offensive or defensive, and it may have place anywhere or everywhere in the game.’
Source: The Art of Chess by James Mason (London, 1898), page xi.
‘We may define the magic word combination in two different ways: as a series of moves having a common object, or as the blending of objective with method.’
Source: Challenge To Chessplayers by Fred Reinfeld (Philadelphia, 1947), page 21.
As shown above, the ‘common object’ idea was mentioned by James Mason on page xi of The Art of Chess (London, 1898).
(9593)
Jean-Pierre Rhéaume (Montreal, Canada) notes that Lasker’s Manual of Chess does not mention the word ‘sacrifice’ in the definition of a combination. From page 123 of the 1927 book and page 109 of the 1932 edition:
‘In the rare instances that the player can detect a variation or net of them which leads to a desirable issue by force, the totality of these variations and their logical connections, their structure, are named a “combination”. And he who follows in his play such a chain of moves is said to “make a combination”.’
We recall a position from Blackburne v Weiss, New York, 1 April 1889:
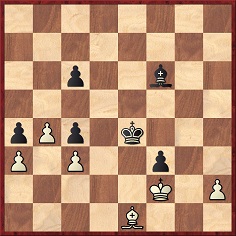
Black to move
52...Bh4+ 53 Kf1 Bxe1 54 Kxe1 Kd3 55 h4 Kxc3 56 h5 Kb3 57 h6 c3 58 h7 c2 59 Kd2 f2 60 h8(Q) c1(Q)+ 61 Kxc1 f1(Q)+ 62 Kd2 Qf2+ 63 Kd3 Qc2+ 64 Ke3 Qc3+ 65 Qxc3+ Kxc3 66 Ke4 Kb3 67 Kd4 Kxa3 68 Kc3 Ka2 69 Kc2 a3 70 Kc1 Kb3 71 White resigns.
On page 140 of The Most Instructive Games of Chess Ever Played (New York, 1965) Irving Chernev commented after 52...Bh4+:
‘This begins a 15-move combination. Despite its length, it is easy enough to visualize and understand it, if we break it down.’
Chernev then listed six stages in ‘the series of ideas’.
After 54...Kd3 Steinitz wrote on page 74 of the New York, 1889 tournament book:
‘The rest speaks for itself, for every move of the opponent is forced. Very likely, Herr Weiss had foreseen the present position and played for it some moves ago, before exchanging bishops, but, undoubtedly, he must have fore-calculated the very end of this game 16 moves later, when he did effect the exchange and relied on the move in the text.’
(10605)
‘It would not be too much of an exaggeration to say that this game is one long combination. This is really a way of paying tribute to White’s inexhaustible ingenuity in conjuring up new attacking ideas.’
Concerning this remark by Fred Reinfeld about Pilnik v Najdorf, Mar del Plata, 24 March 1942 on page 202 of Great Brilliancy Prize Games of the Chess Masters (New York, 1961), see C.N. 11192.
Leonard McLaren (Onehunga, New Zealand) quotes from page 89 of Learn Chess Tactics by John Nunn (London, 2003):
‘... now we focus exclusively on situations in which the winning idea depends on two or more tactical elements. In this book we use the word “combination” to describe such situations but, as with many chess terms, there is no generally accepted definition of “combination” and you should be aware that other authors may use this word in a different sense ...
There is no clear dividing line between a “tactic” and a “combination”, since there is a whole spectrum of difficulty from one-move tactics to massively complex multi-move combinations.’
(10623)
From page 6 of Chess World, January 1967, at the end of an article entitled ‘How to Advance in Chess (2)’ by C.J.S. Purdy, under the heading ‘Purdy, Iconoclast’:
‘My later contribution to chess theory was to point out the bunkum inherent in a priori theories like Z-B’s [Znosko-Borovsky’s] force-space-time one and to show that the proper way to examine chess was to start from the game itself, not to impose something upon it from outside. Thus I started to examine the moves and the rules. Above all, I pointed out that almost the whole basis of chess is the rule that each player must move in turn and only one thing at a time. This makes it entirely different from war and explains why such enormous advantage results if one side can face his opponent with the often impossible task of doing two things at once. Not impossible always, for one move will sometimes do two things. But often. Combinations are all based on that rule.
For years I searched around for a true definition of a combination – there have been at least a dozen attempts – and finally realized that a definition was unnecessary. And why? Because combinations can be split up into something simpler, namely threats. Thus I arrived at my most important dictum:
Threats are the basis of winning chess.’
From the Introduction to Logical Chess Move by Move by Irving Chernev (various editions, with different page numbers):
‘The master does not search for combinations. He creates the conditions that make it possible for them to appear.’
(11418)
To the Chess Notes main page.
To the Archives for other feature articles.
Copyright: Edward Winter. All rights reserved.