Edward Winter
Numerous players treat chess problems with indifference or, even, hostility. The matter was discussed by Reuben Fine in his Introduction (pages v-vii) to Irving Chernev’s Chessboard Magic! (New York, 1943):
‘There are some who deprecate the problemist’s art; it does not improve one’s game, they tell you. At times devotees – rather lamely – try to defend the problem by maintaining that it sharpens the imagination or whets the appetite for combinations – and convince nobody, least of all themselves. The problem is a separate province, in some ways as difficult and as complex as the regular game. It needs no justification – qui s’excuse s’accuse. It stands or falls by the pleasure you derive from it – and I need hardly add my small voice to the booming testimony that it can be great.’
Chessboard Magic! was an anthology of endgame studies, and Fine also commented in his Introduction:
‘I have met many who care very little for the ordinary problem; I have never known any who were not overjoyed and bewitched by endings.’
Players may become attracted to the world of the ‘ordinary problem’ by several means. Some of Samuel Loyd’s spectacular compositions provide an irresistible introduction, and players are often enthusiastic about problems composed by prominent over-the-board masters. Many examples, the work of such figures as Bogoljubow, Euwe, Keres, Lasker, Nimzowitsch, Pillsbury and Schlechter, can be found from the entry on ‘Problems by players’ in our Factfinder. It is also of interest to note the masters’ solving skills, and a number of concrete examples are given in Steinitz Stuck and Capa Caught. Moreover, the problem field has some outstanding figures whose names are insufficiently recognized by chess enthusiasts. One of them is discussed in our feature article ‘Genius’.
Is it possible, though, to offer a basic range of chess problems which are likely to delight newcomers and, even, those players who have traditionally steered clear of this domain? We raised the matter with one of the world’s leading experts, Michael McDowell (Westcliff-on-sea, England). He has kindly made the selection below, and all the explanations and annotations (in italics) are his.
Vincent L. Eaton
Chess Life, 1952

b6B/r5R1/R1n1Pk2/3Q4/5P1b/8/8/7K (7+5)
Mate in two
The problem is solved by a classic paradoxical key move, 1 Qh5, threatening 2 Qg6. Charged with mating Black on the second move, White gives the king an escape square while allowing the knight to discover check. A random move of the knight opens a rook guard on e6 and allows a cross-check, 2 Rb7. The knight can close the path to b7 by moving to e7, but blocking the square allows a second cross-check, 2 Rg2. If the king captures on e6, White delivers a pin-mate, 2 Qe5, and the final defence, 1...Rxg7, leads to a second pin-mate, 2 Qf7.

The above photograph of Vincent Lanius Eaton comes from page 190 of the June 1962 Chess Review.
Anatoly G. Kuznetsov
Special Honourable Mention, 64, 1996

8/P4P1Q/2P1P1p1/K1PkBR2/3PRP2/1N6/B2P4/2N5 (16+2)
Mate in two
The four defences are met by mating moves to different corner squares. This kind of idea is easy to conceive, but it requires great ingenuity to find a matrix that works. 1 Rg5. 1…Kxc6 2 a8(Q); 1…Kxe6 2 Bh8; 1…Kxe4 2 Qh1; 1…Kc4 2 Na1.
Milan Vukcevich
First Prize, StrateGems, 1998

5nbq/6p1/4p3/8/6N1/3QP3/PPKP1PPR/RB4k1 (12+6)
Mate in three
Another spectacular key move, 1 Qh7, sacrifices the queen to three pieces, two of which give check. The threat is 2 Rh1+ Kxg2 3 Qe4. The captures of the queen are met by moves of the king to different squares, determined by the need to avoid discovered checks on the second move. In the sideline variation 1…Kf1 the queen performs a switchback. 1…Qxh7+ 2 Kc3 Qxh2 3 Be4; 1…Bxh7+ 2 Kb3 Kf1 3 Bd3; 1…Nxh7 2 Kd3 and 3 Bc2; 1…g6 2 Rh1+ Kxg2 3 Qb7; 1…Kf1 2 Rh1+ Ke2 3 Qd3; 1…Ng6 2 Kd3.
J. Graham Campbell
London Tourney, 1862

3K4/3B3N/n2pNp2/2pk1p2/2pb1Bp1/2n3Q1/2P5/4R3 (8+10)
Mate in three
In the diagram most black moves are met by immediate mate. The exceptions are 1...Be5, met by 2 Rd1+, and 1...Ne4, which needs attention. The deeply-hidden key move is 1 Rc1, preparing 1...Ne4 2 Qb3 (threatening 3 Qb7) 2…cxb3 3 c4. An old-time classic by a composer who was considered one of the strongest British amateur players in the 1850s.
Johannes Kohtz and Carl Kockelkorn
Honourable Mention, Le Palamède, 1865
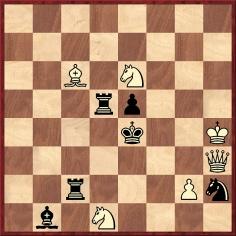
8/8/2B1N3/3rp3/4k2K/7Q/2r3Pn/1b1N4 (6+6)
Mate in five
Despite the open position, most of the black pieces are fixed, defending against immediate mate. Knight moves allow 2 Qf3, while the c2 rook prevents knight mates at c3 and f2. The bishop is free, but takes four moves to liberate Black’s position by capturing on c6. White needs a plan to cope with the bishop, but is equally restricted by the need to maintain the mating threats in order to control the black force. His one free piece is the king, which uses the full length of the solution to perform a slow line clearance 1 Kh5 Ba2 2 Kh6 Bb3 3 Kh7 Ba4 4 Kh8 Bxc6 5 Qh7. If Black checks on the second move by 2...Ng4+, White continues with 3 Kg5 or Kg6, mating next move.
Stefan Schneider
First Place, Austria v Switzerland composing match, 1977

8/1K1R4/pp3p2/8/1p3Np1/4Q3/2pppn1r/2qbkrb1 (4+15)
Mate in five
Potential mates at d2, d3 and g2 are prevented by queen, knight and rook respectively. White would like to build up on e2, but 1 Re7 is useless, and attempting to line the pieces up in the right order by 1 Qe8 is too slow, as it frees Black’s queen. The surprising key move is 1 Ka8, vacating the seventh rank to threaten 2 Rh7 and 3 Rxh2, but allowing a check. 1...Rh8+ is met by 2 Qe8. Now after 2...Rxe8+ 3 Ka7 Black cannot prevent mate on g2 in two moves at most. If the rook returns to h2 White has gained time for 3 Re7, and Black cannot prevent 4 Rxe2+ Bxe2 5 Qxe2. 1 Kb8 fails because after 1…Rh8+ 2 Qe8 Bh2 pins the knight. Similarly 3 Kb7 fails after 3…Rb8+ 4 Kxb8 Bh2.
N. Maksak and V. Rossinsky (after A. Kraemer)
Shakhmaty v SSSR, 1969

5r1k/5Ppr/5p1p/6bp/1R4Q1/8/5RKn/6n1 (5+10)
Mate in five
In many longer directmate problems White must resort to short threats to keep Black tied up. Here 1...g6 will free Black’s position, so White threatens mate immediately with 1 Rb8. 1...g6 is met by 2 Rxf8+ Kg7 3 Qe6 Kxf8 4 Qe8+, so Black’s best defence is to capture. White continues with 2 Rb2, again threatening mate. If the rook returns to f8, 3 Qb4 mates in a further two moves (other rook moves along the rank succumb to 3 Qb4 or other moves), so again capturing is best. After 2...Rxb2+ 3 Qe2 is the final decoy, and after 3...Rxe2+ 4 Kh1 a promotion mate cannot be prevented.
Leonid I. Kubbel
Shakhmaty v SSSR, 1950 or 1948?

2R5/5N1B/1p1pN3/1P2p1p1/p3P2r/Kp1kP1r1/2p5/n1B1R1bb (10+13)
Mate in seven
A striking idea from one of the great all-rounders. Kubbel was equally proficient as a problem and study composer. 1 Kb4 threatens 2 Rc3 mate, and entices the h4 rook to selfpin – 1…Rxe4+. 2 Rc4 threatens 3 Bxe4+ Bxe4 4 Rc3, and 2…Rg4 allows mate in two by 3 Nd4. In the main variation all four escape routes of the e4 rook are blocked, three times by sacrifice. After 2…Rxe3 3 Rd4+ exd4 4 Nf4+ gxf4 5 Ne5+ dxe5 the bishop can safely unpin the rook and mate by 6 Bg8 Rxe1 7 Bc4.
Note: this problem was published posthumously, and there is a doubt about the correct source, as the information in the two main Kubbel collections differs.
From the 1 October 1911 Deutsches Wochenschach:

Norman Macleod
First Prize, Mat, 1983

k2N1n2/P6p/1B6/4P2r/p1pPKP2/qp1pP3/rPp1N2p/4b2B (11+13)
Mate in eight
White will mate if he can move his king off the long diagonal. However, if he advances 1 Kd5, threatening 2 Kxc4, Black has a defence 1...c1(Q) 2 Nxc1 Qxb2, guarding g2. White eliminates this queen promotion defence by first of all going into reverse. 1 Kf3 (threat 2 Kg4) 1...Rh4 2 Kg2 (threat 3 Kf1) 2...dxe2 3 Kf3 (threat 4 Kxe2) 3...c1(N). Now the advance of the king works. 4 Ke4 Rh5 5 Kd5 (threat 6 Kxc4) 5...Qb4 6 Kc6 (threat 7 Kc7) 6...Qe7 7 Kb5+ Qb7 8 Bxb7.
Thomas Brand and Norbert Geissler
Third Prize, Die Schwalbe, 1993

6q1/r5pr/4p1Kp/1p2p1nP/1PR1p3/4p3/7k/1b4b1 (4+14)
Helpmate in five
In helpmates Black begins and helps White to mate in the stipulated number of moves. The amusing idea of the joint composition needs no explanation. The white rook is reduced to shuffling across the board, one step at a time. 1 Ra2 Rd4 2 Rg2 Rxe4 3 Ba2 Rf4 4 Ne4+ Rg4 5 Ng3 Rh4.
Markus Ott
First Prize, Schach-Aktiv, 1993
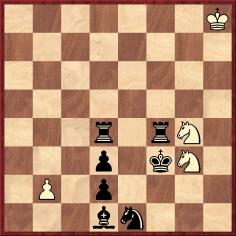
7K/8/8/8/3r1rN1/3p1kN1/1P1p4/3bn3 (4+7)
Helpmate in three (two solutions)
The experienced solver immediately wonders why the outlying white pawn is present. It takes only two moves by each side to set up a mate, the configurations being king on e2 and rook on f1 with the g3 knight mating on d4, or king on e3 and knight on f3 with the g4 knight mating on d1. However, the king must move before the square blocker, and unfortunately he cannot make the first move. It turns out that in each solution the first move must be made by the piece which is standing on the mating square. As this leaves a guard on the mating square the white pawn’s function becomes clear – to shut off the black piece. The solutions are 1 Ra4 Nf5 2 Ke2 b4 3 Rf1 Nd4 and 1 Ba4 Nf2 2 Ke3 b3 3 Nf3 Nd1. The perfect construction and perfectly matching solutions make this a fine example of the genre. Note how 1...Nf5 prevents the f4 rook from playing a northwards waiting move.
Mark Kirtley
First Prize, The Problemist, 1986

3Q4/p7/PP3p2/R4P2/1pP2p1P/N3BN2/kr2BK1P/4R3 (14+6)
Selfmate in eight
Selfmates, where White plays to force Black to deliver mate, may seem counterintuitive to the player but they are entertaining to solve. The solution to Mark Kirtley’s problem falls into two parts: White first brings the black force under control and then constructs the mating position. This involves all eight white pieces returning to their starting squares – a memorable achievement. 1 Nb1+ Kb3 2 Qd1+ Rc2 3 Bc1 axb6 4 Ra1 b5 5 Rh1 bxc4 6 Ke1 c3 7 Ng1 f3 8 Bf1 f2.
This article originally appeared at ChessBase.com.
The Kirtley problem was given in C.N. 1361 by Paul Valois (Leeds, England) on the theme of retreating moves (discussed in C.N.s 1323, 4090 and 4097).
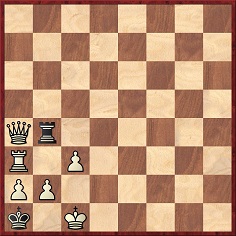
See too Letters and Numbers in Chess Problems. It includes the following mate-in-two position which was given in C.N. 11645 under the heading ‘An ingenious problem’:
To the Chess Notes main page.
To the Archives for other feature articles.
Copyright: Edward Winter. All rights reserved.